Pressure is a key element in diving. During your Open Water course you’ve learnt how pressure affects volume and density. Do you remember?
Pressure in physics (symbol: P) is defined as a force perpendicular to a surface and exerted on an area. In diving theory we talk about atmospheric pressure to refer to the pressure on land and hydrostatic pressure (from Greek hudōr ‘water’) when we talk about the pressure of the water as we descend. Depending on your dive site, the atmospheric pressure can be 1 ATM or less if you do altitude diving (please ask your dive center for more information about the atmospheric pressure at the dive site and consider taking further education on altitude diving). To simplify the matter in this post I will consider an atmospheric pressure of 1 ATM at sea level and salty water diving.
The deeper you go the more pressure increases and you feel this pressure because you need to equalise your ears. At 10m/33ft in salty water you and your diving equipment are subjected to 1 ATM atmospheric pressure plus 1 ATM hydrostatic pressure for a total of 2 ATA or absolute pressure. At 20m/66ft the absolute pressure is therefore 3ATA and so on.

Why do we need to know the absolute pressure at a given depth? Because pressure has consequences on how gases behave: since we need to breathe underwater and air (or Nitrox) is a gas mix, we need to know what happens to the air that we’re breathing and its effects on our body.
So what happens to a gas when pressure increases? In diving theory we distinguish between a flexible container (e.g. a balloon or your lungs) and a non-flexible container (e.g. the tank).
According to Boyle’s Law, if the temperature remains constant, the volume of a gas is inversely proportional to the absolute pressure. In simple words: at 2 ATM the volume of a gas is half (or 1/2). At 3 ATM it is 1/3 and so on. This is easy to see if you bring an empty plastic bottle (flexible container) with you while you descend. The keyword here is “empty”. The bottle is not really empty, but it’s full of air and you seal it by screwing the lid. At 10m/33ft (2 ATA) the plastic bottle will crush to half of its original size, at 20m/66ft (3 ATA) it will crush even more to one third of its original size and at 30m/99ft (4 ATA) it will be hard to believe that there’s still air in it because it will be one fourth of its original size.
 But what happens to our tank then? I’ve never seen a tank crush to one third of its original size! Thank goodness that doesn’t happen! 😀 The tank is a non-flexible container because the material it’s made of (steel or aluminium) doesn’t behave like plastic. However the gas contained in the tank changes its behaviour in terms of density. In physics density is the mass of a substance per unit volume. You can say that density is like the concentration of a specific substance. Imagine to make coffee using instant coffee powder. Depending on how many teaspoons of coffee powder you add to your hot water, you make a weak or a strong coffee. The mass is the number of teaspoons of coffee powder per unit volume represented by your cup of hot water. At the beginning of your dive you know that your tank is full. The deeper you go the more dense the gas in your tank becomes. Basically all the molecules of oxygen (O2) and the atoms of Nitrogen (N) get closer together. And specifically, at 2 ATA the gas density is twice as much, at 3 ATA it’s 3 times and so on. You can see a summary of pressure, volume and density in the table below here.
But what happens to our tank then? I’ve never seen a tank crush to one third of its original size! Thank goodness that doesn’t happen! 😀 The tank is a non-flexible container because the material it’s made of (steel or aluminium) doesn’t behave like plastic. However the gas contained in the tank changes its behaviour in terms of density. In physics density is the mass of a substance per unit volume. You can say that density is like the concentration of a specific substance. Imagine to make coffee using instant coffee powder. Depending on how many teaspoons of coffee powder you add to your hot water, you make a weak or a strong coffee. The mass is the number of teaspoons of coffee powder per unit volume represented by your cup of hot water. At the beginning of your dive you know that your tank is full. The deeper you go the more dense the gas in your tank becomes. Basically all the molecules of oxygen (O2) and the atoms of Nitrogen (N) get closer together. And specifically, at 2 ATA the gas density is twice as much, at 3 ATA it’s 3 times and so on. You can see a summary of pressure, volume and density in the table below here. 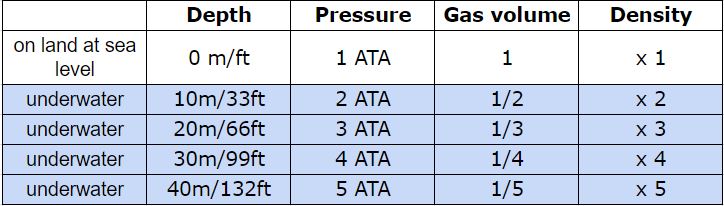 This means that with every breath that you take from your regulator at 20m/66ft, you’re actually breathing 3 times more O2 and N than you would on land. Is that bad? Well, yes and no. According to Henry’s Law, the amount of gas that dissolves into a liquid at a given temperature is directly proportional to the partial pressure of that gas. Right, let’s translate that in simple words.
This means that with every breath that you take from your regulator at 20m/66ft, you’re actually breathing 3 times more O2 and N than you would on land. Is that bad? Well, yes and no. According to Henry’s Law, the amount of gas that dissolves into a liquid at a given temperature is directly proportional to the partial pressure of that gas. Right, let’s translate that in simple words.
 Air is composed by 21% of O2 and 79% of N -I know, it’s an approximation and we’re not taking into consideration Hydrogen, but bear with me, please 🙂 On land, where the pressure is 1 ATM, air has a total pressure of 1 ATM. According to Dalton’s Law, the total pressure exerted by a mixture of gases is equal to the sum of the pressures of each of the different gases making up the mixture – each gas acting as if it alone were present and occupied the total volume. This means that on land the partial pressure of oxygen (PPO2) is 0.21 ATA and the partial pressure of nitrogen (PPN) is 0.79 ATA because 0.21 + 0.79 = 1. Now let’s take our tank of air underwater at 10m/33ft. The pressure here is 2 ATA, which means that our PPO2 is 0.21 x 2 = 0.42 ATA and our PPN is 0.79 x 2 = 1.58 ATA. If we sum the two partial pressures the result should be 2 ATA. As a matter of fact, 0.42 + 1.58 = 2. Yeah! 🙂 I’m sure that now you know how to calculate the partial pressure of oxygen and nitrogen at 20m/66ft or 30m/99ft. 😉 Remember how to do this calculation because it’s important for your Nitrox course! 😉
Air is composed by 21% of O2 and 79% of N -I know, it’s an approximation and we’re not taking into consideration Hydrogen, but bear with me, please 🙂 On land, where the pressure is 1 ATM, air has a total pressure of 1 ATM. According to Dalton’s Law, the total pressure exerted by a mixture of gases is equal to the sum of the pressures of each of the different gases making up the mixture – each gas acting as if it alone were present and occupied the total volume. This means that on land the partial pressure of oxygen (PPO2) is 0.21 ATA and the partial pressure of nitrogen (PPN) is 0.79 ATA because 0.21 + 0.79 = 1. Now let’s take our tank of air underwater at 10m/33ft. The pressure here is 2 ATA, which means that our PPO2 is 0.21 x 2 = 0.42 ATA and our PPN is 0.79 x 2 = 1.58 ATA. If we sum the two partial pressures the result should be 2 ATA. As a matter of fact, 0.42 + 1.58 = 2. Yeah! 🙂 I’m sure that now you know how to calculate the partial pressure of oxygen and nitrogen at 20m/66ft or 30m/99ft. 😉 Remember how to do this calculation because it’s important for your Nitrox course! 😉  Let’s go back to Henry’s Law and specifically to the part about a gas dissolving into a liquid. The most common example of a gas dissolved into a liquid is carbon dioxide (or CO2) in soda drinks. During bottling, CO2 is added at a high pressure and then the can or bottle is sealed. As soon as you open a can or a bottle of carbonated beverage you immediately hear the fizz: because of the lower pressure (atmospheric pressure) the CO2 that was trapped inside the can or bottle starts getting out of your drink. Leave the can there for a few hours or for a day and your drink will lose all the bubbles. So we can say that if the pressure increases, more gas can be dissolved into a liquid and if the pressure decreases the gas in excess will leave the liquid. Now, you probably know that an adult human body is made of up to 70% of water, so you know where I’m going right? Put together what you’ve just read about partial pressure of gases and the fact that our body is mainly composed of water and you have the explanation of Henry’s Law: the amount of gas that dissolves into a liquid at a given temperature is directly proportional to the partial pressure of that gas. With what we know so far let’s take our air tank and go to 10m/33ft:
Let’s go back to Henry’s Law and specifically to the part about a gas dissolving into a liquid. The most common example of a gas dissolved into a liquid is carbon dioxide (or CO2) in soda drinks. During bottling, CO2 is added at a high pressure and then the can or bottle is sealed. As soon as you open a can or a bottle of carbonated beverage you immediately hear the fizz: because of the lower pressure (atmospheric pressure) the CO2 that was trapped inside the can or bottle starts getting out of your drink. Leave the can there for a few hours or for a day and your drink will lose all the bubbles. So we can say that if the pressure increases, more gas can be dissolved into a liquid and if the pressure decreases the gas in excess will leave the liquid. Now, you probably know that an adult human body is made of up to 70% of water, so you know where I’m going right? Put together what you’ve just read about partial pressure of gases and the fact that our body is mainly composed of water and you have the explanation of Henry’s Law: the amount of gas that dissolves into a liquid at a given temperature is directly proportional to the partial pressure of that gas. With what we know so far let’s take our air tank and go to 10m/33ft:- every breath we take is composed by double the amount of oxygen and nitrogen compared to a breath on land because of the increased pressure (2 ATA) and therefore the gas density (x 2),
- more gas will dissolve into our body, both oxygen and nitrogen because of Henry’s Law.
- every breath that we take contains 3 times the amount of oxygen and nitrogen that we would breathe on land (because of a pressure of 3 ATA and gas density x 3)
- a lot more gas will dissolve into our body because of Henry’s Law.
 Ok, so no problem, right? Actually you can’t decrease pressure in a very short time or the gas in excess will shoot out in bubbles. Take the carbonated drink that I mentioned earlier and shake it before you open it: the soda will shoot out and make a mess. I guess that you want to avoid the same mess when you start your ascent, right? The key is to observe an ascent rate of no more than 9m/30ft per minute. This speed (or less) in addition to a 3-minute safety stop, should give your body enough time to release some of the gas in excess without the formation of the big bubbles that are responsible for any form of decompression sickness (DCS) or barotrauma. Exactly: “should” because there’s no guarantee of 100% safety without consequences after one or multiple dives even if you follow all the best practices. Your body will go on releasing the gas in excess during your surface interval and that’s why it’s important that you don’t start another descent before the surface interval recommended by the tables and/or by your diving computer. On the other side, not following the rules gives you a very high chance of getting “the bends”, so the choice is yours. Actually you know what? It’s not! You want to risk your life? Pick another sport! Diving is not an individual sport (it can be if you’re a self-reliant diver, but that’s another story): recreational diving is for buddy teams which means that if your buddy wants to skip the safety stop or ascend too fast (and now you should know the consequences of that!), not only he/she will put his/her life at risk but yours as well! Do you really want to go diving with this person? Don’t be afraid to speak up! One mistake can cause serious consequences for the rest of your life! Enjoy diving and remember: safety first! 🙂 If you enjoyed this post, please consider sharing it!
Ok, so no problem, right? Actually you can’t decrease pressure in a very short time or the gas in excess will shoot out in bubbles. Take the carbonated drink that I mentioned earlier and shake it before you open it: the soda will shoot out and make a mess. I guess that you want to avoid the same mess when you start your ascent, right? The key is to observe an ascent rate of no more than 9m/30ft per minute. This speed (or less) in addition to a 3-minute safety stop, should give your body enough time to release some of the gas in excess without the formation of the big bubbles that are responsible for any form of decompression sickness (DCS) or barotrauma. Exactly: “should” because there’s no guarantee of 100% safety without consequences after one or multiple dives even if you follow all the best practices. Your body will go on releasing the gas in excess during your surface interval and that’s why it’s important that you don’t start another descent before the surface interval recommended by the tables and/or by your diving computer. On the other side, not following the rules gives you a very high chance of getting “the bends”, so the choice is yours. Actually you know what? It’s not! You want to risk your life? Pick another sport! Diving is not an individual sport (it can be if you’re a self-reliant diver, but that’s another story): recreational diving is for buddy teams which means that if your buddy wants to skip the safety stop or ascend too fast (and now you should know the consequences of that!), not only he/she will put his/her life at risk but yours as well! Do you really want to go diving with this person? Don’t be afraid to speak up! One mistake can cause serious consequences for the rest of your life! Enjoy diving and remember: safety first! 🙂 If you enjoyed this post, please consider sharing it!